算法学习：常用设计思想解读

前言

在前面几篇文章中，我们介绍了几个常用的数据结构。根据我的理解，数据结构帮助我们对需要解决的问题进行，而算法就是我们解决问题方案的具体。它包括对问题的分析及研究（建立描述问题的数学模型），然后根据一些策略和思想制定出解决问题的方案。

算法设计思想

算法设计思想，是指在设计算法时所遵循的指导原则和方法。常见的算法设计思想有以下几种：

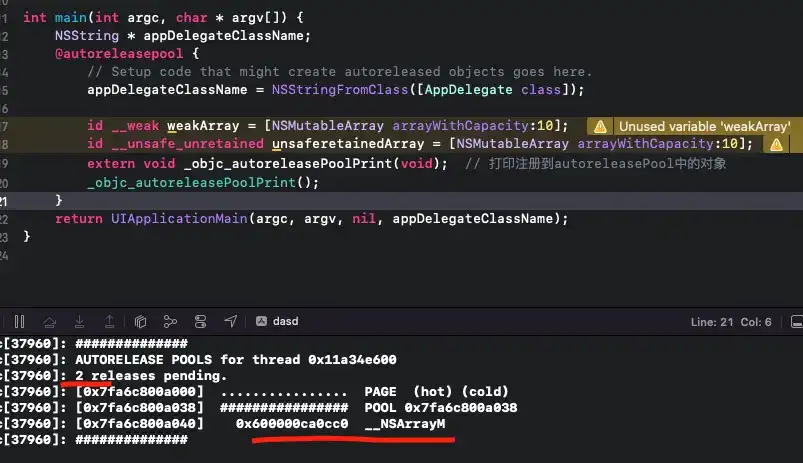
1. 贪心思想

贪心思想是一种简单而有效的算法设计思想。它的基本思想是，在当前情况下做出最优的选择，并以此为基础做出后续的选择。贪心算法的特点是，它只考虑当前的局部最优解，而不考虑全局的最优解。贪心算法的优点是简单易懂，计算量小。但贪心算法的缺点是，它有时不能得到全局最优解。

2. 动态规划思想

动态规划思想是一种解决最优化问题的常见算法设计思想。它的基本思想是，将一个大问题分解成若干个小问题，然后逐个求解这些小问题，最后将这些小问题的解组合成大问题的解。动态规划思想的优点是，它可以保证找到最优解。但动态规划思想的缺点是，它的时间复杂度和空间复杂度通常较高。

3. 分治思想

分治思想是一种将问题分解成若干个子问题的算法设计思想。它的基本思想是，将一个大问题分解成若干个小问题，然后分别解决这些小问题，最后将这些小问题的解组合成大问题的解。分治思想的优点是，它可以将一个复杂的问题分解成若干个简单的问题，从而简化问题的求解过程。但分治思想的缺点是，它有时需要额外的空间来存储子问题的解。

4. 回溯思想

回溯思想是一种解决组合优化问题的常见算法设计思想。它的基本思想是，从一个初始解出发，枚举所有可能的解，并在枚举过程中不断回溯，直到找到一个满足约束条件的最优解。回溯思想的优点是，它可以保证找到最优解。但回溯思想的缺点是，它的时间复杂度和空间复杂度通常较高。

5. 分支限界思想

分支限界思想是一种解决组合优化问题的常见算法设计思想。它的基本思想是，从一个初始解出发，枚举所有可能的解，并在枚举过程中不断剪枝，即丢弃那些不满足约束条件的解，直到找到一个满足约束条件的最优解。分支限界思想的优点是，它可以减少枚举的解的数量，从而降低算法的时间复杂度和空间复杂度。但分支限界思想的缺点是，它仍然需要枚举所有可能的解，因此它的时间复杂度和空间复杂度仍然较高。

6. 随机算法

随机算法是一种使用随机数来解决问题的算法设计思想。它的基本思想是，利用随机数来生成候选解，然后通过某种方法选择一个最优的候选解。随机算法的优点是，它可以快速地找到一个近似最优解。但随机算法的缺点是，它不能保证找到最优解。

结语

以上介绍了算法设计思想，包括贪心思想、动态规划思想、分治思想、回溯思想、分支限界思想和随机算法等。这些算法设计思想是解决算法问题的重要工具。学习并掌握这些算法设计思想，可以帮助我们快速地学习算法，并设计出高效的算法。