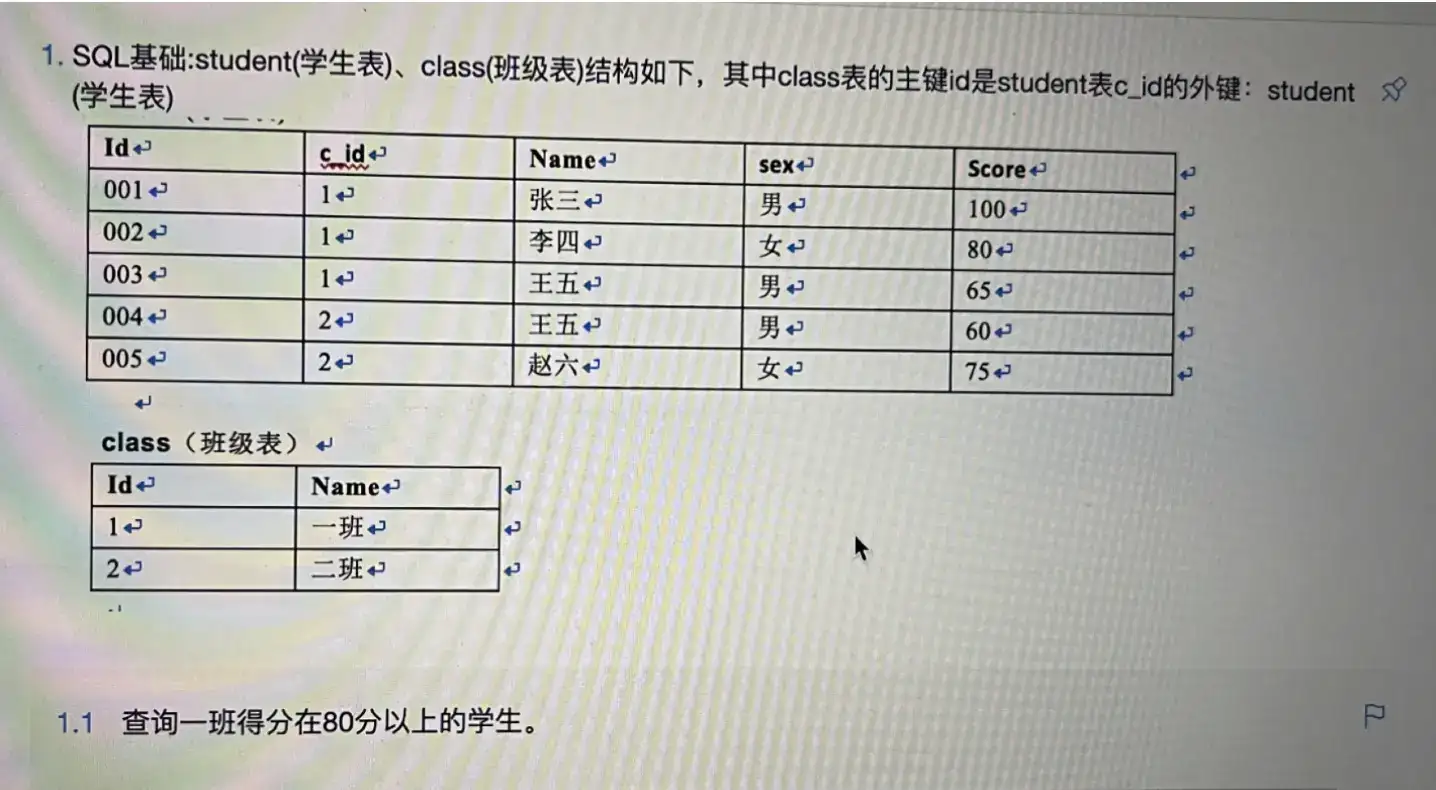
BF算法详解：步步深入理解模式匹配原理

引言：

在计算机科学领域，字符串匹配算法扮演着至关重要的角色。BF算法，全称暴力匹配算法（Brute Force），以其朴素直接的原理和高效的实现而著称。它广泛应用于文本搜索、模式识别、生物信息学等诸多领域。本文将以可视化的方式，深入浅出地讲解BF算法的运作机制和原理，帮助读者透彻地理解模式匹配的奥秘。

BF算法原理：

BF算法的核心思想非常直观，它以蛮力穷举的方式，逐个比较模式串中的字符与主串中相应位置的字符，直到模式串与主串完全匹配或主串完全被遍历完。这种逐个比较的过程，就像一只蚂蚁沿着主串从头到尾巡视，与模式串中的字符进行一对一的对比，直至找到匹配。

可视化示例：

为了便于理解，我们以一个可视化的例子来说明BF算法的过程。假设主串为"toneornot"，模式串为"no"。

步骤 1： 将模式串与主串对齐，从主串的第一个字符开始。

主串：toneornot
模式串：no

步骤 2： 比较模式串的第一位"n"和主串的第一位"t"，发现不相等。

步骤 3： 将模式串向右移动一位，与主串的第二个字符对齐。

主串：toneornot
模式串：  no

步骤 4： 比较模式串的第一位"n"和主串的第二个字符"o"，发现不相等。

步骤 5： 继续向右移动模式串，直至模式串与主串完全对齐或主串完全被遍历完。

主串：toneornot
模式串：    no

步骤 6： 在主串中未找到与模式串匹配的子串。

时间复杂度：

BF算法的时间复杂度为 O(mn)，其中 m 为主串的长度，n 为模式串的长度。最坏情况下，当模式串与主串完全不匹配时，算法需要遍历整个主串，比较次数达到 O(mn)。

应用场景：

BF算法虽然时间复杂度较高，但在实际应用中，当模式串相对较短时，算法的效率仍然很不错。例如，在文本搜索中，如果要查找一个短语，BF算法可以快速找到匹配的结果。此外，BF算法的实现简单、易于理解，在教学和入门级应用中也得到了广泛的应用。

优化改进：

虽然BF算法有着较高的时间复杂度，但也有多种优化改进的方法，例如：

• KMP算法（Knuth-Morris-Pratt算法）： 利用失败函数加速匹配过程，时间复杂度优化为 O(n+m)。
• BM算法（Boyer-Moore算法）： 预处理模式串，跳跃匹配，时间复杂度优化为 O(mn)。

这些优化改进的方法可以显著提升BF算法的效率，使其在更广泛的场景中得到应用。

结语：

BF算法是一种基本的字符串匹配算法，以其简单、直观的原理而著称。虽然它的时间复杂度较高，但在模式串较短或主串较小的情况下，算法仍然表现出良好的效率。通过可视化的讲解和实际应用的举例，本文深入剖析了BF算法的运作机制和时间复杂度，为读者提供了一个全面而清晰的理解。